Jacobi–Anger expansion
In mathematics, the Jacobi–Anger expansion (or Jacobi–Anger identity) is an expansion of exponentials of trigonometric functions in the basis of their harmonics. It is useful in physics (for example, to convert between plane waves and cylindrical waves), and in signal processing (to describe FM signals). This identity is named after the 19th-century mathematicians Carl Jacobi and Carl Theodor Anger.
The most general identity is given by:[1][2]
and
where 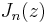 is the n-th Bessel function. Using the relation
is the n-th Bessel function. Using the relation 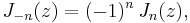 valid for integer n, the expansion becomes:[1][2]
valid for integer n, the expansion becomes:[1][2]
The following real-valued variations are often useful as well:[3]
Notes
References
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 9", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 355, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_355.htm.
- Colton, David; Kress, Rainer (1998), Inverse acoustic and electromagnetic scattering theory, Applied Mathematical Sciences, 93 (2nd ed.), ISBN 978-3-540-62838-5
- Cuyt, Annie; Petersen, Vigdis; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008), Handbook of continued fractions for special functions, Springer, ISBN 978-1-4020-6948-2
External links
- Weisstein, Eric W.. "Jacobi–Anger expansion". MathWorld — a Wolfram web resource. http://mathworld.wolfram.com/Jacobi-AngerExpansion.html. Retrieved 2008-11-11.
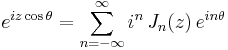
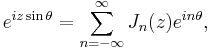
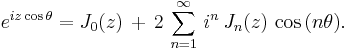
![\begin{align}
\cos(z \cos \theta) &= J_0(z)%2B2 \sum_{n=1}^{\infty}(-1)^n J_{2n}(z) \cos(2n \theta),
\\
\sin(z \cos \theta) &= -2 \sum_{n=1}^{\infty}(-1)^n J_{2n-1}(z) \cos\left[\left(2n-1\right) \theta\right],
\\
\cos(z \sin \theta) &= J_0(z)%2B2 \sum_{n=1}^{\infty} J_{2n}(z) \cos(2n \theta),
\\
\sin(z \sin \theta) &= 2 \sum_{n=1}^{\infty} J_{2n-1}(z) \sin\left[\left(2n-1\right) \theta\right].
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/fb31adb3b7fa05878a4697400b24563d.png)